개요
https://papers.nips.cc/paper/2013/hash/af21d0c97db2e27e13572cbf59eb343d-Abstract.html
Earth mover's distance 혹은 optimal transport distance는 계산할 때 많은 연산량이 필요하다: 최소 필요 연산 량은 \( d^3 \log d\) (d는 point 의 수)라고 한다.
이 논문에서는 EMD를 entropy term으로 regularization을 한다. 이 regularization term 때문에 Sinkhorn fixed point iteration 알고리즘으로 regularized된regularized 된 EMD를 계산할 수 있게 된다. Sinkhorn fixed point iteration 알고리즘은 matrix product만 사용하고 linear convergence를 보이기 때문에 빠르게 계산할 수 있다. 이 regularized 된 EMD를 Sinkhorn distance라고 이 논문에서 부른다.
추가로 MNIST같은 dataset에 대해서 이 regularized distance가 classification에 더 유용하다는 보너스 성질도 있다.
Optimal transport 리뷰
Transport polytope 정의
- \( \Sigma_d := \{x \in \mathbb{R}^d_+| x^T 1_d = 1\} \). 여기서 \(1_d \)는 component가 다 1인 d-dimensional vector. 즉 component의 합이 1인 non-negative real number로 이뤄진 벡터. 즉 \( \Sigma_d \)의 원소는 확률 벡터로 해석 가능. 참고로 \( \Sigma_d\)는 (d-1)-dimensional simplex로도 해석 가능.
- \( U(r,c):=\{ P\in \mathbb{R}^{d \times d}_+ | P 1_d=r, P^T 1_d=c \} \). 여기서 r, c는 두 개의 확률 벡터: \( r, c \in \Sigma_d \). r과 c의 transport polytope 라고 부른다. polytope라고 불리는 이유는 각 조건들이 simplex의 조건들이라 결국 polyhedral set이기 때문.
- 확률적 해석: X, Y가 각각 r, c의 distribution을 갖는 확률 분포라고 하면 U(r,c)는 가능한 모든 joint probability of X,Y. \( P \in U(r,c)\)이면 \( p(X=i,Y=j) = p_{ij}\) 라고 표기.
- h: entropy, KL: KL-divergence. \(r \in \Sigma_d, P,Q \in U(r,c)\)일 때:
\( h(r) = -\sum_i r_i \log r_i\), \( h(P) = -\sum_{ij} p_{ij} \log p_{ij}\), \( KL(P||Q) = \sum_{ij}p_{ij} \log \frac{p_{ij}}{q_{ij}}\)
Optimal transport distance
- M: d x d dimensional cost matrix
- 두 분포 r, c가 있을 때 r 분포를 c 분포로 보낼 때 필요한 cost가 M으로 기술된다고 하자. 그러면 cost는 \( \langle P,M\rangle \). 여기서\( \langle \cdot, , \cdot \rangle\)는 Frobenius dot-product
- Optimal transport distance / Earth mover's distance는 \( d_M(r,c):= \min_{P\in U(r,c)} \langle P, M \rangle\)
- 이 양이 거리의 정의를 만족하려면 M도 metric matrix여야 함: \( M \in \mathbb{R}^{d\times d}_+\), \( m_{ij}=0\) iff i=j (positivity),\( m_{ij} \le m_{ik} + m_{kj}\) (triangular inequality), \( m_{ij}=m_{ji}\) (symmetry)
- worst case complexity: \( O(d^3 \log d)\)
- 지난 포스트 <2023.02.03 - [개념 정리] - [정리] Earth mover's distance> 참고
Sinkhorn Distance = Optimal transport distance with entropic constraints
Sinkhorn distance 정의
- 다음과 같은 inequality가 있다: \( h(P) \le h(r) + h(c)\), 여기서 \( r,c \in \Sigma_d, P\in U(r,c)\).
- \( P=rc^T\)인 경우 equality 만족
- 다음과 같은 집합을 정의 하자: \( U_\alpha (r,c) := \{ P \in U(r,c) | KL(P||rc^T \le \alpha )\} = \{ P \in U(r,c) | h(P) \ge h(r) + h(c) - \alpha \} \in U(r,c)\)
- 풀어서 말하면 r, c로 이뤄진 independent table \( rc^T\)와 가까운 joint probability distribution의 집합
- KL divergence 정의를 쓰면 쉽게 \( KL(P||rc^T) = h(r) +h(c) - h(P)\)인 것을 보일 수 있어서 위에 등호 성립
- Entropy는 concave 하기 때문에 (\(h(\lambda P + (1-\lambda)Q) \ge \lambda h(P) + (1-\lambda) h(Q)\)), \( U_\alpha (r,c)\) 는 convex set이다. 참고로 이때 \( U_\alpha (r,c)\)도 convex 집합이라는 사실을 사용했다.
- \( KL(P||rc^T)\)은 mutual information이라고도 해석이 가능하기 때문에 (random variable X가 r이란 distribution을 따르고 Y라는 random variable이 c라는 distribution을 따른 다는 해석 하에) mutual information이 적은 집합이라고 해석 가능. 이것이 말이 되는 게 mutual information은 한 변수에 대해서 알면 다른 변수에 대한 정보를 얼마나 알 수 있는지를 수치화한 것인데, \( rc^T\)는 r과 c의 mutual information이 최소이기 때문에 (서로 독립적), 이 distribution에 가까울수록 mutual information이 작을 수밖에 없음. 또는 r과 c의 entropy에 비해서 얼마나 entropy가 큰 distribution 들인가로 해석 가능
- Sinkhorn distance: \( d_{M,\alpha}(r,c) := \min_{P\in U_\alpha (r,c)} \langle P, M \rangle \): mutual information에 제한을 둔 상태에서 계산한 optimal transport distance. 좋은 이유:
- 계산하기 더 편함 (뒤에 추가 설명)
- optimal transport의 solution은 U(r,c)의 vertex인 극단적인 solution: d x d matrix with only at most 2d-1 non-zero entries. Constraint를 두면 solution이 덜 극단적임.
Sinkhorn distance의 성질
- \( \alpha\)가 충분히 클 때: \( d_{M,\alpha} = d_M\)
- \( \alpha = 0\) 일 때: \( d_{M,0} = r^T M c\) . M이 Euclidean distance matrix이면 \( d_{M,0}\)은 negative definite이고 \( e^{-t d_{M,0}}\)는 positive definite for all t>0
- \( \alpha\ge 0 \)이고 M이 metric matrix이면 \( d_{M,\alpha}\)은 symmetric & triangle inequality를 만족함. 하지만 positivity는 만족 안 함. \( (r,c) \rightarrow 1_{r\neq c} d_{M,\alpha}(r, c)\)는 positivity도 만족해서 distance function임.
- positivity를 만족 안 하는 것은 쉽게 알 수 있음: \( \alpha\)가 매우 작다고 하자. h(r)>0이면 (h(r)=0인 경우는 r이 단 한 element만 1이고 나머지가 0인 distribution) metric matrix의 성질 (off-diagonal은 양수) 때문에 \( d_{M,\alpha}(r,r)>0\)
증명은 논문 참고
Sinkhorn algorithm으로 sinkhorn distance 계산
이제 다음과 같이 정의되는 dual Sinkhorn divergence를 고려해 보자:
\[ d^\lambda_M(r,c) = \langle P^\lambda,M \rangle, \quad P^\lambda = \min_{P\in U(r,c)} (\langle P,M \rangle - \frac{1}{\lambda}h(P))\]
- Sinkhorn distance는 optimal transport distance에 \( 0 \le h(P) + h(r) + h(c) - \alpha \)라는 constraint를 준 것이기 때문에 strong duality theory를 적용하면 (https://people.eecs.berkeley.edu/~elghaoui/Teaching/EE227A/lecture8.pdf) 각 \( \alpha \)마다 \( d_{M,\alpha} (r,c) = d^\lambda_M(r,c)\)인 \( \lambda \)를 찾을 수 있다.
- \( \alpha\)가 주어졌을 때 \( P_\alpha \)는 \( U_\alpha(r,c)\)의 boundary에서 나타나는데, 이유는 다음과 같다: 우선 \( \langle P, M\rangle\)이라는 함수는 P에 대해서 concave이면서 convex이다. 중요한 것은 convex 함수이다는 것이고, \( U_\alpha(r,c)\)는 convex set이기 때문에, 만약 boundary에서 minimum이 아니면 말이 안 된다.
- 다음 figure이 Sinkhorn distance와 dual Sinkhorn divergence를 잘 설명해 준다

이제 dual sinkhorn divergence를 계산하는 방법을 알아보자 (dual sinkhorn divergence와 sinkhorn distance의 정확한 연관성은 duality 이상으로 논문에서 다루지 않는다)
- \( \lambda>0 \)일 때 \( P^\lambda\)는 유일하고 \( P^\lambda = \textrm{diag}(u) K \textrm{diag}(v) \) 꼴로 적을 수 있다. \( u,v \in \mathbb{R}^{+d}\), unique up to multiplicative factor, \( K = e^{-\lambda M}\) (element-wise exponential). 추가로 K가 strictly positive일 때 Sinkhorn's theorem에 의하면 \( \textrm{diag}(u) K \textrm{diag}(v) \in U(r,c) \)로 적을 수 있는 경우는 unique하다.
- 따라서 \( K = e^{-\lambda M}\) 인 행렬을 \( \textrm{diag}(u) K \textrm{diag}(v) \in U(r,c) \)로 변환할 수 있는 u,v를 찾으면 문제를 풀 수 있다.
- 이러한 u,v는 Sinkhorn's fixed point iteration을 사용해서 구할 수 있다
Sinkhorn Knopp Algorithm: (Philip A. Knight의 "The SInkhorn-Knopp Algorithm: Convergence and Applications" 참고)
- non-negative matrix A가 있으면 \( P=DAE\)가 doubly stochastic matrix \( \sum_{i}A_{ij} =1,\sum_{j}A_{ij} =1 \)가 되게 만드는 알고리즘이다 (D, E는 diagonal matrix).
- 번갈아 가면서 row와 column을 1로 normalize하는 것이 아이디어다
- 이 알고리즘에서 \( D_0 A E_0 \rightarrow D_1 A E_1 \rightarrow D_2 A E_2 \rightarrow ... \)일 때 doubly stochastic matrix로 수렴한다. 여기서 \( D_0=I, E_0=I\).

Variant of Sinkhorn fixed point algorithm

- \( r_0=e\)일 때 결국 Sinkhorn Knopp algorithm이랑 같다고 한다
- \( c=1/A^T r, r=1/Ac\)를 반복해서 계산하는 것과 같다. 여기서 /는 element-wise division.
위에서 소개한 Sinkhorn Knopp algorithm은 doubly stochastic matrix 에 관한 것이지만 저자들이 transport polytope에도 적용 가능한가보다 (저자들이 특별히 이 부분에 대해서는 코멘트를 하지는 않음). 저자들에 의하면 위와 비슷하게
- \( u = r/Kv, v=c/K^Tu\)를 반복하면 된다고 한다.
- 논리는 같다: row를 더하면 r이 나오고 column을 더하면 c가 나오도록 iterative하게 계속 normalize하는 것이다.
정리하면 다음과 같은 알고리즘이 나온다:

MNIST classification
dual Sinkhorn divergence를 기반으로 Kernel을 만들어 (\( e^{-d/t}\), d는 distance, t>0는 hyperparameter)로 사용해서 SVM을 하면 좋은 결과를 얻을 수 있다고 한다. 실험 디테일은 논문 참고
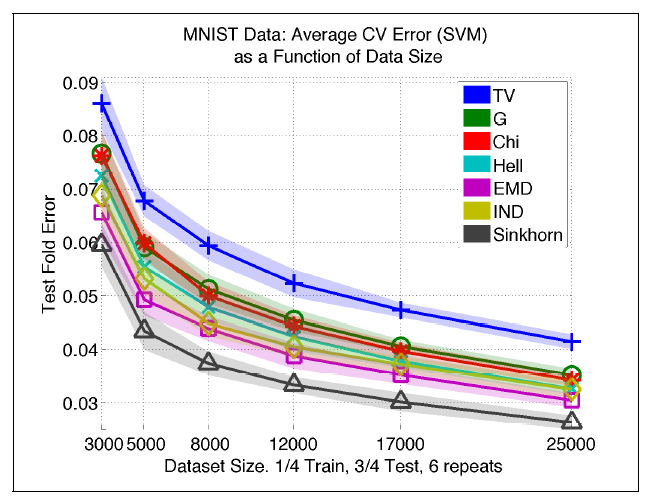
계산 속도
위에 소개한 알고리즘은 GPU에서 계산하기 좋다.
보통 iteration을 수십번 하면 converge하는 결과를 얻었다고 한다. MNIST 실험에서는 20번으로 고정해서 실험을 했다고 한다.
\( \lambda \)가 크면 EMD와 가까워지면서 수렴할 때 까지 더 오래 걸린다

'논문 리뷰 > others' 카테고리의 다른 글
| 기초 diffusion probabilistic model 이론 공부 로드맵 (1) | 2024.06.16 |
|---|---|
| [간단 리뷰] RepOptimizer (RepOpt-VGG) (0) | 2023.06.29 |
| [간단 리뷰] RepVGG: Making VGG-style ConvNets Great Again (0) | 2023.06.18 |
| [논문 리뷰] 잡다한 지식 모음 (0) | 2023.02.01 |