다이나믹 프로그래밍이란 어떠한 문제를 소문제들로 나누고, 소문제들을 풀어서 결과 값을 저장하고, 원래 문제를 풀 때 소문제의 결괏값을 사용하는 방법론을 말한다.
다이나믹 프로그래밍으로 풀 수 있는 대표적인 문제가 피보나치 수열을 계산하는 문제다 (풀이를 이해하는 것도 쉬운 편이다; https://leetcode.com/problems/fibonacci-number/). 피보나치 수열 \( F_0 = 0, F_1 = 1, F_{n}=F_{n-1}+F_{n-2}\)로 정의되는 수열이다 (0, 1, 1, 2, 3, 5, 8, 13...). 우선 약간 무식하게 제귀함수로 풀어보자:
def fib(n):
if n <= 1:
return n
else:
return fibonacci(n-1) + fibonacci(n-2)n=6인 경우 다음과 같이 계산된다 (밑에 살짝 생략):
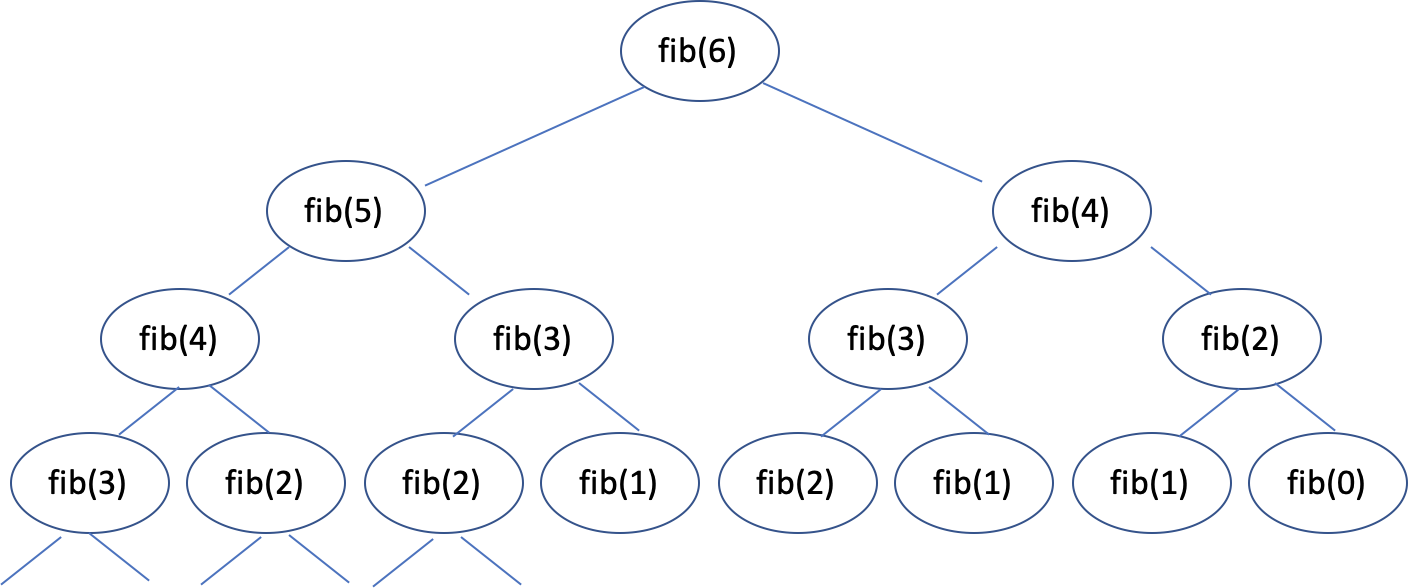
이런 풀이 방식은 계산 복잡도는 기하급수적이라서 비효율적이다: \(O(1.6180^n\)다 (https://www.geeksforgeeks.org/time-complexity-recursive-fibonacci-program/).
반면에 각 \( F_n\)을 구하기 위해서 이전 값들 \( F_{n-1}, F_{n-2}\)가 필요한데, 이 값들을 매번 계산하지 않고 저장해두면 효율적으로 피보나치 수열을 계산할 수 있다. 이런 방식들은 O(n) 계산 복잡도를 갖는다.
Top-down approach (하양식/메모이제이션): n에서부터 더 작은 n에 대한 \( F_n\) 값들을 계산하는 방식으로 진행:
class Solution:
Fib = collections.defaultdict(int)
def fib(self, n: int) -> int:
if n <= 1:
return n
if self.Fib[n]:
return self.Fib[n]
self.Fib[n] = self.fib(n-1) + self.fib(n-2)
return self.Fib[n]Bottom-up approach (상향식/타뷸레이션): 작은 n부터 계산해서 순차적으로 더 큰 n에 대해서 \( F_n\)을 계산한다
class Solution:
Fib = collections.defaultdict(int)
def fib(self, n: int) -> int:
self.Fib[0] = 0
self.Fib[1] = 1
for i in range(2,n+1):
self.Fib[i] = self.Fib[i-1]+self.Fib[i-2]
return self.Fib[n]
참고로 다익스트라 알고리즘 같은 경우 출발점부터 방문한 노드까지 거리를 최소화해서 저장하고, 다른 노드들 까지 거리를 최소화하는 방식으로 설계되어있기 때문에 다이나믹 프로그래밍 기법에 해당돤다 ([알고리즘] 다익스트라 알고리즘 (+LeetCode 1514)).
다음 글:
'알고리즘' 카테고리의 다른 글
| [알고리즘] 다이나믹 프로그래밍 (문제편 2: 백준 2098 외판원 순회) (0) | 2023.04.02 |
|---|---|
| [알고리즘] 다이나믹 프로그래밍 (문제편 1: 배낭 문제) (0) | 2023.04.01 |
| [알고리즘] 투 포인터 (+LeetCode 5) (0) | 2023.03.26 |
| [알고리즘] 구간 합 (+LeetCode 1314) (0) | 2023.03.25 |
| [알고리즘] 이진 탐색 (+LeetCode 33) (0) | 2023.03.07 |