728x90
728x90
개요
논문 링크: https://arxiv.org/abs/1704.03976 (Virtual Adversarial Training: A Regularization Method for Supervised and Semi-Supervised Learning)
Adversarial training 기법을 semi-supervised learning에 적용한 기법이라고 이해하면 된다. Labeled data에 대해서는 평소대로 학습을 하고, unlabeled data + labeled data에 대해서는 다음과 같이 adversarial training을 한다: 모델이 뱉어내는 output (classification probability)를 가장 잘 망가뜨리는 perturbation을 input에 더하고, 이런 perturbation에 대하여 모델이 robust 하도록 학습시킨다. 이런 학습 방식은 모델이 input에 대해서 smooth 하게 변하도록 regularization해주는 효과가 있다.
방법
Adversarial training 간단 리뷰
- \( x_l\): input data
- \( \theta\): 모델 파라미터
- \( q(y|x_l)\): input data에 대한 ground truth label (확률 분포로 나타냄)
- \( p(y|x_l,\theta)\): neural network가 예측하는 label 확률 분포
- Adversarial loss:
\[ L_{adv} (x_l,\theta) = D[q(y|x_l), p(y|x_l+r_{adv},\theta)] \quad (1)\]
\[ r_{adv} = \textrm{arg} \max_{r; ||r|| \le \epsilon} D[q(y|x_l),p(y|x_l+r,\theta)] \quad (2)\]- \( D[p,p']\): 분포 p, p' 간 차이를 구해주는 함수; 예를 들어 cross entropy.
- 식 (2)는 풀기 어렵기 때문에 실제로는 gradient를 사용해서 근사하는 것이 편하다. 식 (2)에서 \( || \cdot ||\)이 \( L_2\)일 때 :
\[ r_{adv} \approx \epsilon \frac{g}{||g||_2}, \textrm{where } g=\nabla_{x_l} D[h(y;y_l),p(y|x_l,\theta)] \quad (3)\]
\( || \cdot ||\)이 \( L_\infty\)일 때 :
\[ r_{adv} \approx \epsilon \textrm{sgn}(g) \quad (4)\]
- \( h(y;y_l): x_l\)의 ground truth label을 one-hot vector로 나타낸 표현 (\(y=y_l\)일 때만 1, 나머지는 0)
Virtual Adversarial Training
- 아이디어는 식 (2), (3)을 labeled & unlabeled data에 적용시키는 것이다.
- 하지만 unlabeled data에 \(x_{ul} \)에 대해서는 \( q(y|x_{ul})\) 정보가 없다
- 그래서 true label distribution q 대신에 현제 모델이 예측하는 label distribution p를 사용해서 식 (2), (3)을 다음과 같이 변형해서 사용한다:
\[ LDS(x_* , \theta) = D[ p(y|x_*,\hat{\theta}), p(y|x_* + r_{vadv} , \theta) ] \quad (5) \]
\[ r_{vadv} = \textrm{arg} \max_{r; ||r||_2 \le \epsilon} D[p(y|x_*,\hat{\theta}), p(y|x_* + r) \quad (6)]\]
- \( p(y|x_*,\hat{\theta})\)가 현제 모델이 예측하는 label
- \( r_{vadv}\): 실제 label이 아닌 현제 모델이 생각하는 (virtual) label을 망가뜨리는 perturbation; 그래서 virtual adversarial training이라고 부름
- LDS는 일종의 local smoothness를 주는 loss
- virtual adversarial loss는 LDS를 데이터 전체에 평균 낸 값:
\[ \mathcal{R}_{vadv} (\mathcal{D}_l,\mathcal{D}_{ul},\theta) = \frac{1}{N_l+N_{ul}} \sum_{x_* \in \mathcal{D}_l, \mathcal{D_{ul}}} LDS(x_*,\theta) \quad (7) \]- 여기서 (\mathcal{D}_l,\mathcal{D}_{ul}) 는 labeled/unlabeled data
- Full loss:
\[ \ell(\mathcal{D}_l,\theta) + \alpha \mathcal{R}_{vadv} (\mathcal{D}_l,\mathcal{D}_{ul}, \theta) \quad (8)\]- \( \ell\)은 labeled data에 대한 negative log likelihood loss
- hyperparameter은 \( \epsilon\) (perturbation 크기), \( \alpha\)가 있는데, 사실 둘 다 비슷한 역할을 해서 \( \alpha\)는 1로 고정하고 \( \epsilon\)만 튜닝해도 괜찮다 (작은 \( \epsilon\)에 대해서 Taylor expansion을 생각하면 이해하기 쉽다)
VAT loss 계산 방법
- 아쉽게도 식 (3)처럼 간단하게 \( r_{vadv}\)를 구할 수 없다: \( D[ p(y|x_*,\hat{\theta}), p(y|x_* + r , \theta) ] \)를 r에 대해서 미분하면 r=0일 때 0이다.
- 하지만 논문에 친절하게 설명되어있듯이 다음과 같이 계산할 수 있다:
\[ r_{vadv} \approx \epsilon \frac{g}{||g||_2} \quad (14)\]
\[ \textrm{where } g = \nabla_r D[p(y|x,\hat{\theta}), p(y|x+r,\hat{\theta})] |_{r=\xi d} \quad (15)\]- \( \xi\)는 작은 상수 (\(10^{-6} \) 사용했다고 한다)
- d는 random 하게 샘플링한 벡터
- \( r_{vadv}\)를 구하면 \( \mathcal{R}_{vadv}\)의 gradient descent는 쉽게 할 수 있다. 따라서 다음과 같은 알고리즘을 얻을 수 있다:

예시) 간단한 문제이긴 하지만 각 class에 대해서 4개의 label만 가지고도 좋은 classification 결과를 얻을 수 있다:
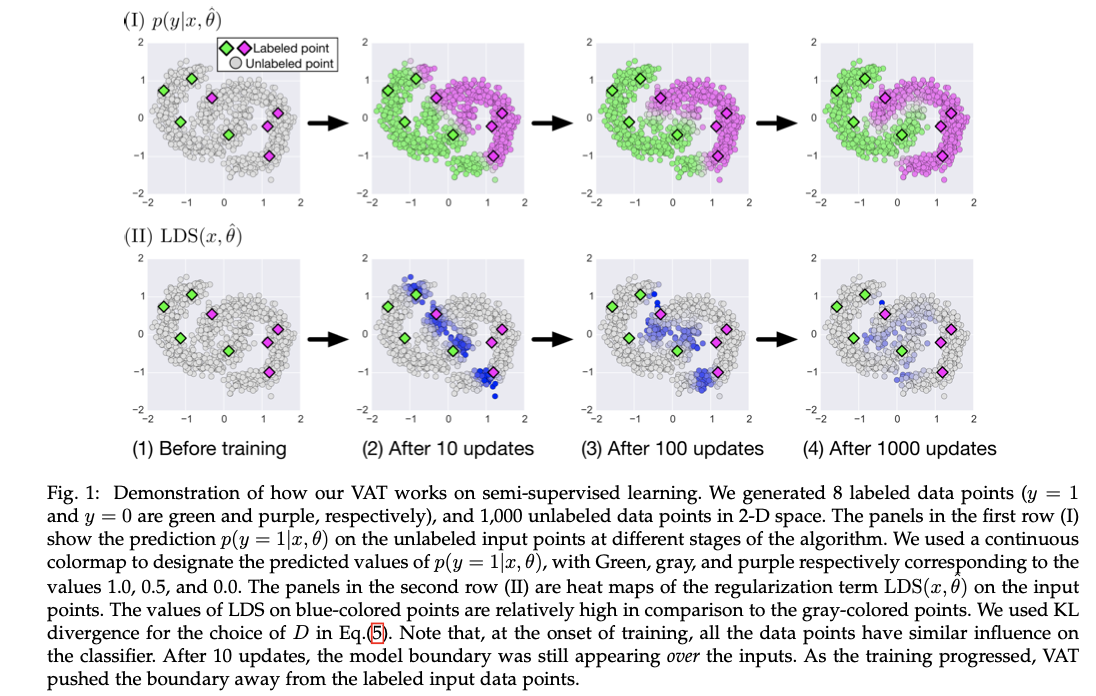
논문에 다양한 실험들이 있는데 관심 있으면 참고.
728x90
728x90
'논문 리뷰 > semi-supervised learning' 카테고리의 다른 글
| [논문 리뷰] Unsupervised Data Augmentation for Consistency Training (0) | 2023.06.03 |
|---|---|
| [논문 리뷰] ReMixMatch (0) | 2023.04.06 |
| [논문 리뷰] MixMatch (0) | 2023.03.22 |
| [논문 리뷰] Mean teachers are better role models (0) | 2023.03.13 |
| [논문 리뷰] Pseudo label (0) | 2023.03.12 |