728x90
728x90
개요
논문 링크: https://arxiv.org/abs/2007.06346
제목: Whitening for Self-Supervised Representation Learning
이전 글:
BYOL에서 어떻게 degenerate solution을 피해 가는지에 대해서 많은 논란이 있었지만, 몇 가지 study에 의하면 적어도 projection / predictor head (MLP)에 있는 Batch Normalization이 중요한 역할을 한다 (https://arxiv.org/abs/2010.00578, https://generallyintelligent.com/research/2020-08-24-understanding-self-supervised-contrastive-learning/).
W-MSE에서는 이러한 관측을 기반으로 우선 feature들을 whitening한 후 positive pair 사이에 MSE loss를 계산한다 (W-MSE). 이렇게 하면 collapse가 생기지 않는다는 것을 발견하였고, W-MSE 기반 self-supervised learning 성능 또한 좋은 편이다. Collapse 피해 가는 방법을 분석한 측면에서 좋은 논문.
방법
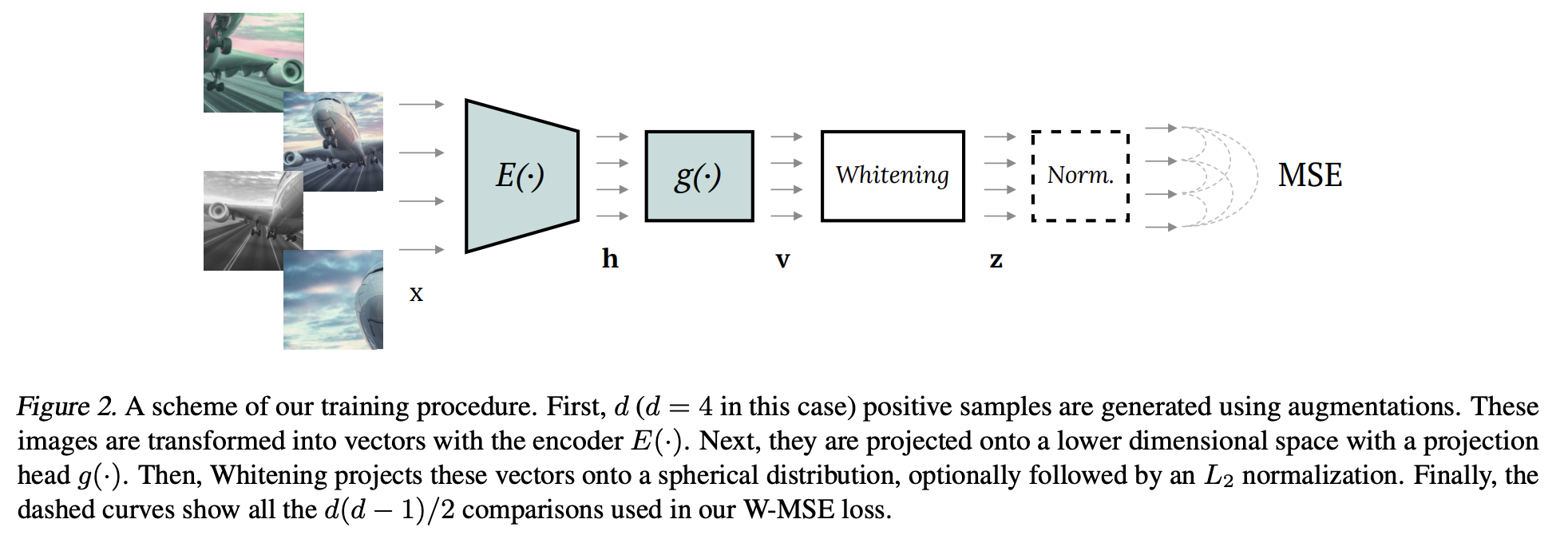
Notation
- \(x\): image
- \( z=f(x;\theta)\): embedding (Figure 2 참고)
- f = encoder = Whitening(g(E(x))).
- E는 ResNet (pooling layer까지)
- g는 MLP (hidden layer 1개, batch norm layer 1개).
- Whitening operation은 뒤에 추가 설명.
- \( \theta\): parameters
W-MSE의 목표


- dist = cosine similarity (식 5), I = identity matrix
- \( z_i, z_j\)는 positive image pair \(x_i,x_j\)에 해당하는 feature.
- cov = covariance
- 이미지 batch를 augmentation해서 z_i를 얻고, 다른 방식으로 augmentation 해서 z_j를 얻는다. 식 (4)는 i batch와 j batch를 따로 whitening 했다는 뜻
- 식 (4) 때문에 degenerate solution을 피해간다 (모든 이미지에 대해서 같은 feature 값을 계산하게 되는 solution)
- 식 (4) 때문에 각 z 의 component들이 linearly independent 하게 된다. 따라서 각 z의 component들은 다른 semantic content를 표현하게 된다
W-MSE 목표의 구체적인 implementation
- 이미지에 random augmentation해서 positive sample들을 얻는다
- random crop, grayscaling, color jittering.
- augmentation parameter은 positive sample마다 random 하게 설정한다
- d = positive sample 수는 2 또는 4를 사용한다. 모든 positive sample pair에 대해서 MSE를 계산한다
- 예) d=2: positive pair = 2개
- 예) d=4: positive pair 6개 (d(d-1)/2 = 6)
- N개의 이미지가 있으면 augmentation을 통해서 각각 d개의 positive sample을 만든다
- 따라서 batch 에 있는 총 이미지 수 K = Nd, batch = \(B= \{ x_1,...,x_K\}\)
- \(V= \{ v_1,...,v_K\}\) (v = g(E(x)))
- \( Whitening (v)= W_V(v-\mu_V)\), \( \mu_V = \frac{1}{K} \sum_k v_k\), \( W_V^TW_V = \Sigma^{-1}_V\), \( \Sigma = \frac{1}{K-1} \sum_k (v_k-\mu_V)(v_k-\mu_V)^T\) = V의 covariance matrix
- 위에서 언급했듯이 whitening까지 한 feature = z (z = Whitening(g(E(x))))
- 이렇게 얻은 feature에 대해서 W-MSE loss 계산 (V에 있는 모든 positive pair에 대해서 summation을 한다)

- W-MSE의 intuition은 밑에 Figure 1 참고

Batch slicing: 추가적인 trick
- 식 6에서 MSE를 계산할 때 \( W_V\)에 의존하게 되는데 (whitening을 하기 때문에), \( W_V\)는 batch 사이 variance가 클 수 있다.
- 높은 variance에 의하여 학습이 잘 안 될 수도 있다. 이러한 variance를 낮추기 위해서 batch slicing을 사용한다
- Batch slicing 하는 방법은 밑에 Figure 3 참고

- Batch slicing의 효과:
- single batch에 대해서 여러 \( W_V^i\)를 사용하기 때문에 W의 high variance를 "평균"내주는 효과가 있다.
- 다른 방식으로 slicing을 해서 (다른 random permutation을 통해) 평균을 내면 더 stable 한 MSE를 계산할 수 있다
추가 implementation detail & 결과
- W-MSE 2, 4는 각각 d=2,4를 의미
- sub-batch size (Fig 3에서 V0,V1 등등의 사이즈) = 128, 256 정도를 사용 (dataset마다 다르다)
- W-MSE loss를 계산할 때 Batch slicing을 1번 또는 4번을 해서 평균 낸다 (dataset마다 다르다)
- Adam optimizer (weight decay = 10^-6)
- epoch, learning rate는 dataset마다 다르게 한다 (epoch: 1000 또는 2000, learing rate는 2 또는 3 x 10^-3). lr scheduler도 사용 (warmup + 학습 후반부에 learning rate decay)
- K = 1024
- g의 hidden layer dimension = 1024
- augmentation의 detail은 논문 참고
linear classifier 결과

추가 결과는 논문 참고
728x90
728x90
'논문 리뷰 > self-supervised learning' 카테고리의 다른 글
| [논문 리뷰] SuperClass (Classification Done Right for Vision-Language Pre-Training) (0) | 2024.11.08 |
|---|---|
| [논문 리뷰] DINO-v1 (Emerging Properties in Self-Supervised Vision Transformers) (0) | 2023.08.13 |
| [논문 리뷰] MeanShift (2) | 2023.05.21 |
| [논문 리뷰] SNCLR (0) | 2023.05.21 |
| [논문 리뷰] self-supervised learning 이 항상 도움될까? (0) | 2023.03.30 |